290th LeetCode Weekly Contest

這次解出 3 題啦

(不過是解出第四題的Hard而不是第三題的Medium www)

但整題還算有進步ㄅ

這次週賽的四個題目：

Intersection of Multiple Arrays

Description:

Given a 2D integer array nums where nums[i] is a non-empty array of distinct positive integers, return the list of integers that are present in each array of nums sorted in ascending order.

Example:

Example 1:

Input: nums = [[3,1,2,4,5],[1,2,3,4],[3,4,5,6]]
Output: [3,4]
Explanation: 
The only integers present in each of nums[0] = [3,1,2,4,5], nums[1] = [1,2,3,4], and nums[2] = [3,4,5,6] are 3 and 4, so we return [3,4].

Example 2:

Input: nums = [[1,2,3],[4,5,6]]
Output: []
Explanation: 
There does not exist any integer present both in nums[0] and nums[1], so we return an empty list [].

Constraints:

1 <= nums.length <= 1000
1 <= sum(nums[i].length) <= 1000
1 <= nums[i][j] <= 1000
All the values of nums[i] are unique.

給一個 2D 陣列要找出在每個每個子陣列都有出現過的數字，並且數字要以升序排好

Concept：

直接開一個map紀錄這個數字出現過幾次（這邊也可以用unordered_map不過符合的數字還要 sort 過）

如果該數字出現的次數與子陣列數量相同：就是符合的數字

Solution：

#define F first
#define S second
#define PB push_back

class Solution {
public:
    vector<int> intersection(vector<vector<int>>& nums) {

        int n = nums.size();

        map<int,int> M;
        for(auto &i:nums){
            for(int &j:i){
                M[j]++;
            }
        }

        vector<int> ans;

        for(auto &i:M){
            if(i.S==n) ans.push_back(i.F);
        }

        return ans;
    }
};

Count Lattice Points Inside a Circle

Description:

Given a 2D integer array circles where circles[i] = [xi, yi, ri] represents the center (xi, yi) and radius ri of the ith circle drawn on a grid, return the number of lattice points that are present inside at least one circle.

Note:

A lattice point is a point with integer coordinates.
Points that lie on the circumference of a circle are also considered to be inside it.

Example:

Example 1:

Ex 1

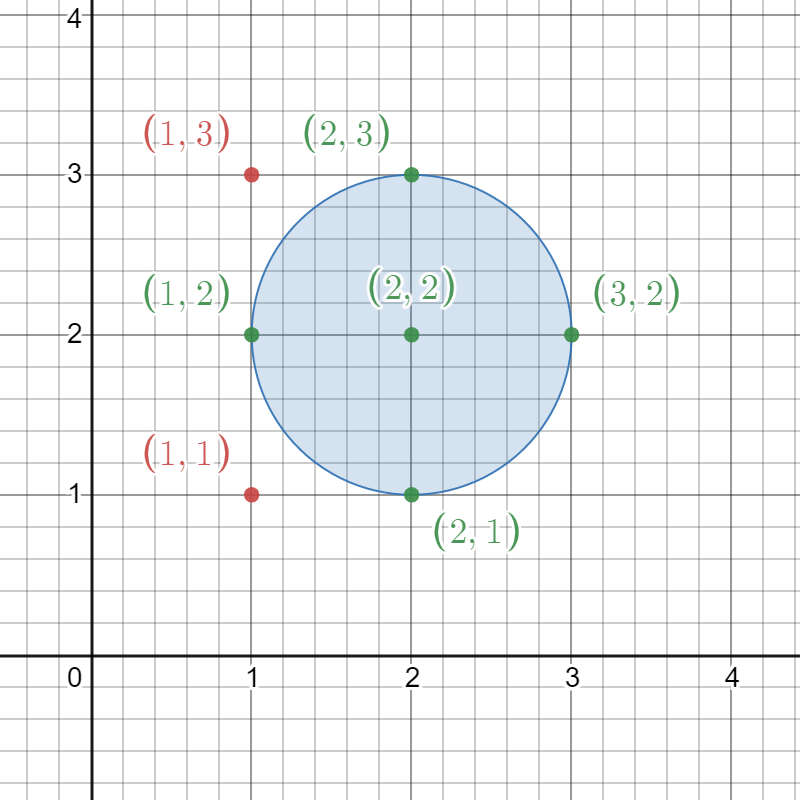
Input: circles = [[2,2,1]]
Output: 5
Explanation:
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.

Example 2:

Ex 2

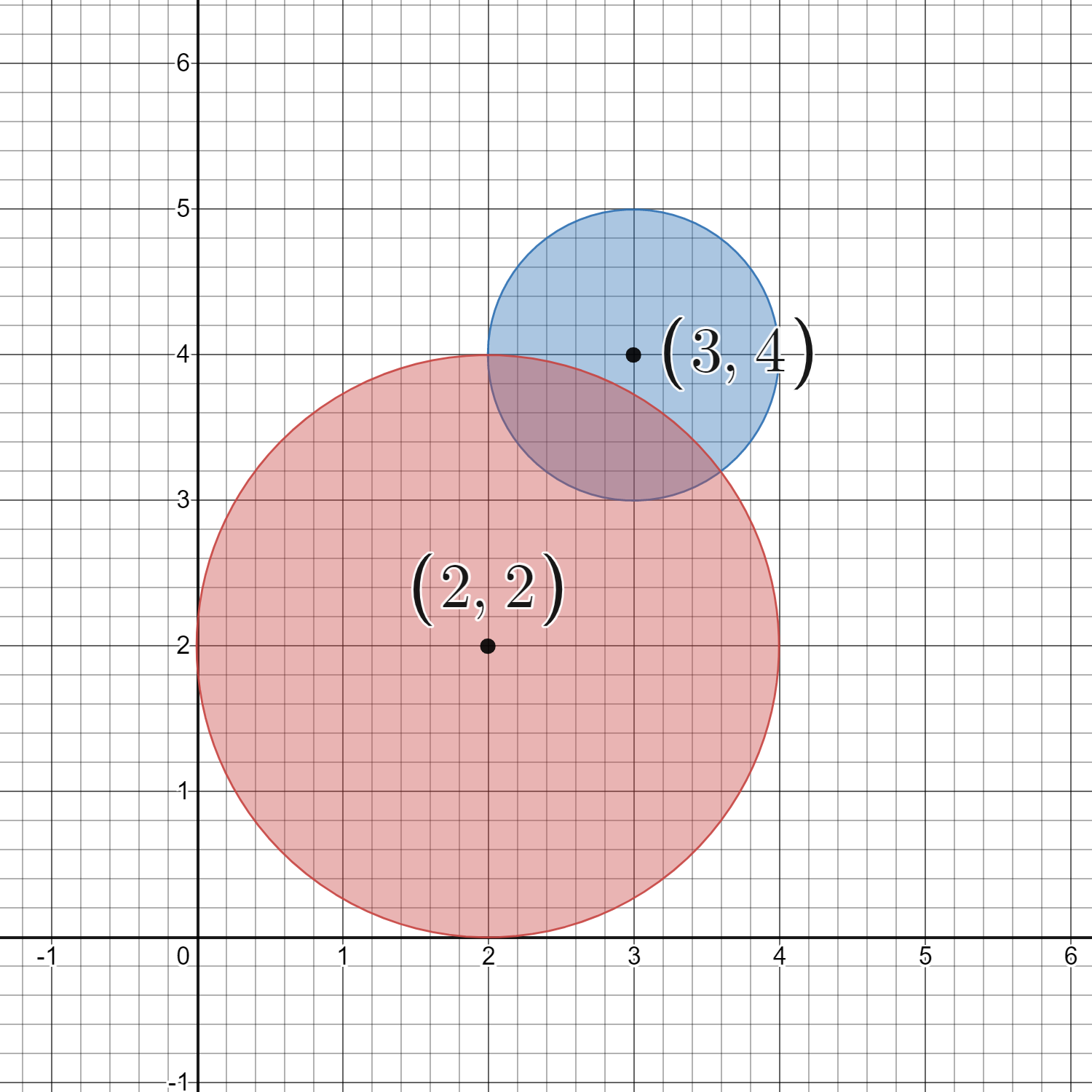
Input: circles = [[2,2,2],[3,4,1]]
Output: 16
Explanation:
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle. 
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).

Constraints:

1 <= circles.length <= 200
circles[i].length == 3
1 <= xi, yi <= 100
1 <= ri <= min(xi, yi)

題目給出很多個圓，每個原有給出中心座標(x,y)和半徑r

要求出每個圓聯集中的整數座標點有幾個

Concept：

要如何求出在一個圓中的整數座標點？

枚舉座標點
畢氏定理

對於每個中心座標為(X,Y)的圓，先枚舉在(i,j)

並且i in range:[X-R,X+R]、j in range:[Y-R,Y+R]

再判斷(i,j)與(X,Y)的距離是否小於等於r

(用dx*dx + dy*dy <= r*r 可以避免小數點誤差)

圓的聯集

用set紀錄所有符合的該圓的座標點

這樣可以去除交集的部份

而聯集的大小恰好會是Set的Size

Solution：

一開始用unordered_map(Hash table)紀錄每個數字出現幾次

typedef pair<int,int> pii;

class Solution {
public:
    int countLatticePoints(vector<vector<int>>& circles) {
        set<pii> Set;

        for(auto &i:circles){
            int X=i[0] , Y=i[1], R=i[2];

            for(int x=X-R;x<=X+R;x++){
                for(int y=Y-R;y<=Y+R;y++){
                    int dx = x-X;
                    int dy = y-Y;

                    if(dx*dx+dy*dy <= R*R ){
                        Set.insert({x,y});
                    }
                }
            }
        }

        return Set.size();
    }
};

Count Number of Rectangles Containing Each Point

Count Number of Rectangles Containing Each Point

Description :

You are given a 2D integer array rectangles where rectangles[i] = [li, hi] indicates that ith rectangle has a length of li and a height of hi. You are also given a 2D integer array points where points[j] = [xj, yj] is a point with coordinates (xj, yj).

The ith rectangle has its bottom-left corner point at the coordinates (0, 0) and its top-right corner point at (li, hi).

Return an integer array count of length points.length where count[j] is the number of rectangles that contain the jth point.

The ith rectangle contains the jth point if 0 <= xj <= li and 0 <= yj <= hi. Note that points that lie on the edges of a rectangle are also considered to be contained by that rectangle.

Exmample:

Example 1:

Ex 1

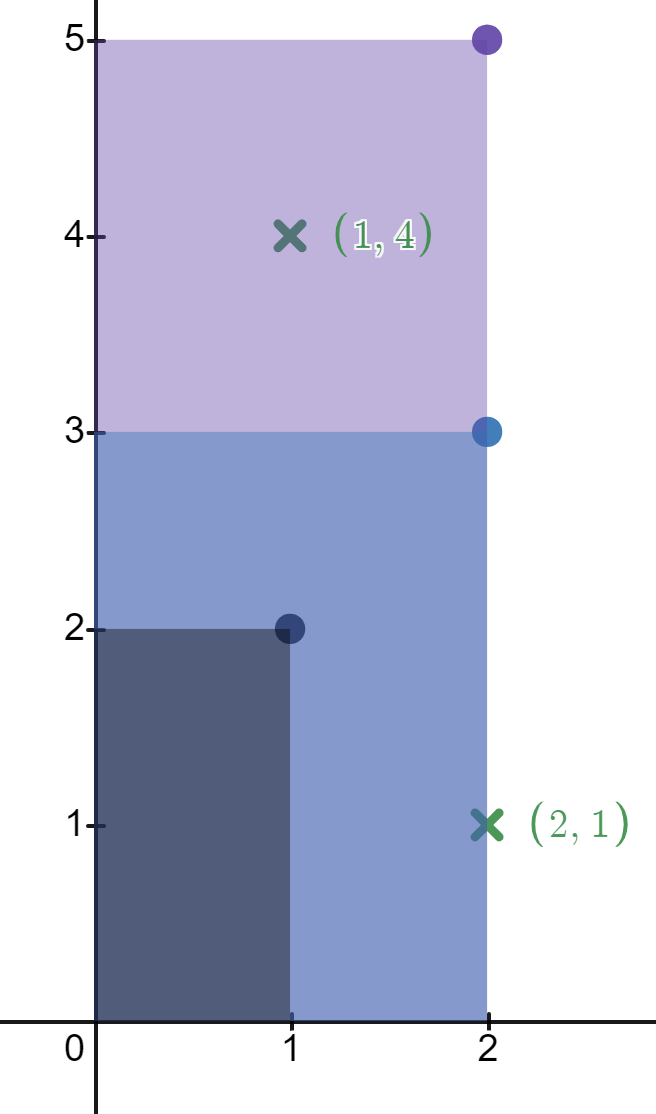
Input: rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
Output: [2,1]
Explanation: 
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return [2, 1].

Example 2:

Ex 2

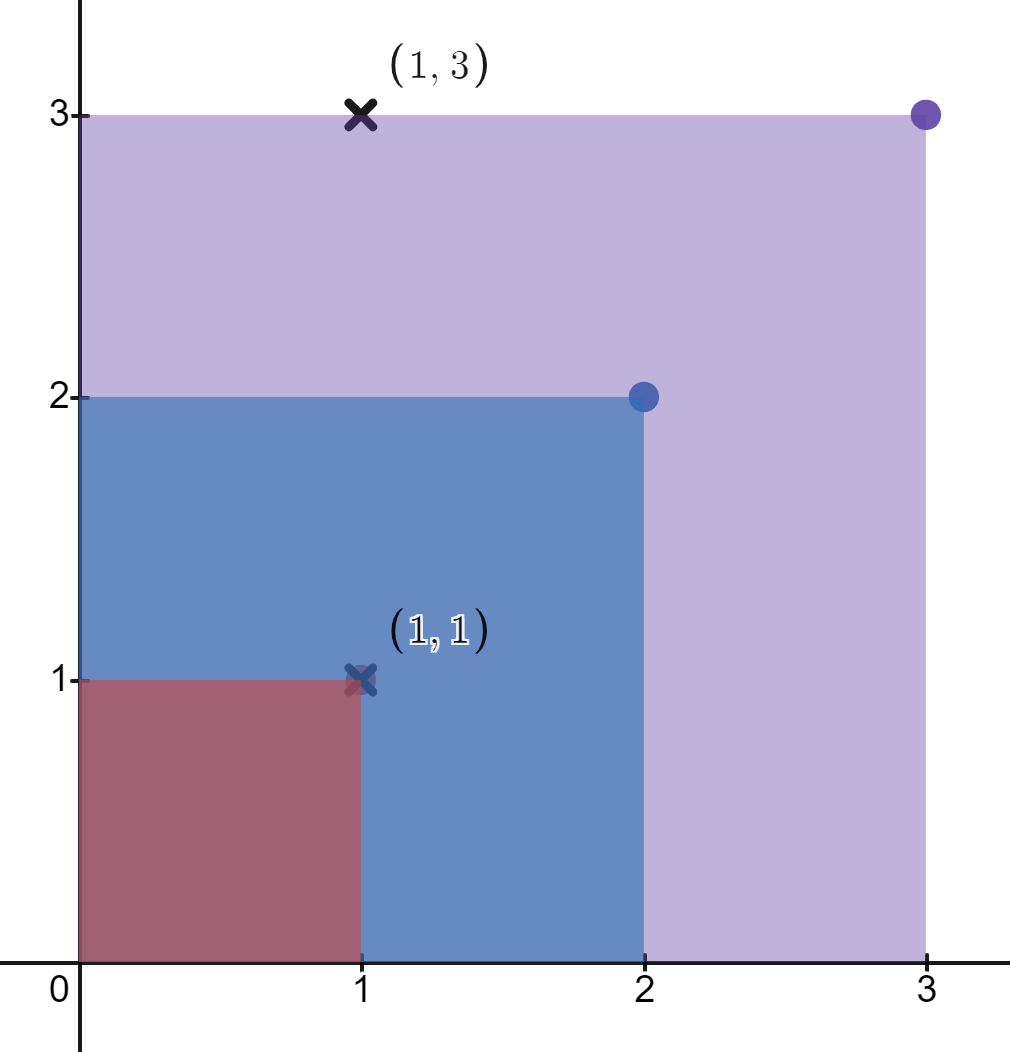
Input: rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
Output: [1,3]
Explanation:
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return [1, 3].

Constraints:

1 <= rectangles.length, points.length <= 5 * 10^4
rectangles[i].length == points[j].length == 2
1 <= li, xj <= 10^9
1 <= hi, yj <= 100
All the rectangles are unique.
All the points are unique.

有rectangles和points兩個陣列，要求出每個points被（ be contained by rectangles）幾個rectangles包含

Concept：

雖然沒有解出來，不過比賽時的分析是對的

分析題目範圍：

先看題目的範圍：

` 1<= posX <= 10^9`

` 1<= posY <= 100 `

所以針對X座標應該要Binary Search，針對Y座標應該Bucket sort就可以了 ( 到這邊為止的分析都是正確的！ )

（但是後來一直被2D Rank Finding的想法綁住，想到需要分治…~~又感覺Leetcode Mudium不會出到那麼難~~）

看了大佬的code，找到實做關鍵：

以 Y 座標做 Bucket sort

開一個2D vector並且index(row)是Y座標

在以該Y座標作為index的vector推入X座標

vector<vector<int> > bucketY(101);
for(auto &P : rect) {
    bucketY[ P[1] ].push_back( P[0] );
}
...

在將每列以X座標sort過（為了之後的二分搜）

for(auto &v : bucketY) sort( range(v) );
...

符合的矩形條件：

rectangle要包含該point :

posY大於等於point.Y
posX大於等於point.X

而該point被包含的rectangles數量會是要符合以上兩個條件的所有rectangles

所以Y座標的起始點是point.Y，然後繼續往比point.Y大的檢查

而X座標就以Binary-Search找到符合的X

而在該Y座標符合條件的矩形數量剛好是：

bucketY[k].end() - lower_bound( range( bucketY[k] ), posX ); ( k in [point.Y , 100 ])

Solution:

#define range(x) x.begin(),x.end()

class Solution {
public:
    vector<int> countRectangles(vector<vector<int>>& rect, vector<vector<int>>& points) {
        vector<vector<int> > bucketY(101);
        for(auto &P : rect) {
            bucketY[ P[1] ].push_back( P[0] );
        }
        for(auto &v : bucketY) sort( range(v) );

        vector<int> ans(points.size());

        int i = 0;
        for(auto &P : points) {
            int posX = P[0], posY = P[1];
            int sum = 0;
            for(int k = posY; k <= 100; k++) {
                sum += bucketY[k].end() - lower_bound( range( bucketY[k] ), posX );
            }
            ans[i++] = sum;
        }
        return ans;
    }
};

Number of Flowers in Full Bloom

Description :

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array persons of size n, where persons[i] is the time that the ith person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.

Example:

Example 1:

Ex 1

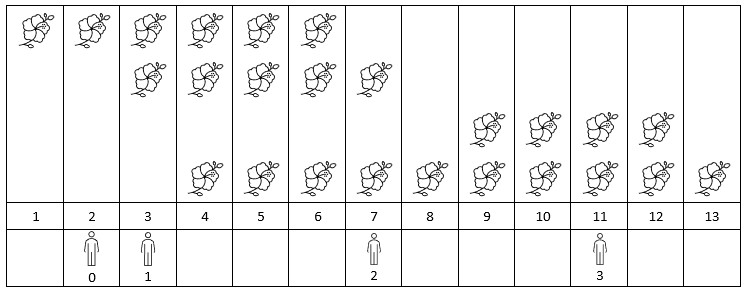
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

Ex 2

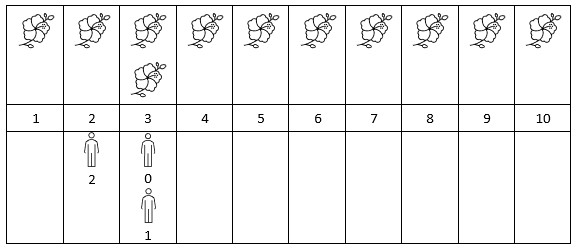
Input: flowers = [[1,10],[3,3]], persons = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Constraints:

1 <= flowers.length <= 5 * 10^4
flowers[i].length == 2
1 <= starti <= endi <= 10^9
1 <= persons.length <= 5 * 10^4
1 <= persons[i] <= 10^9

可以看成：給很多線段（每個線段的座標範圍是[st,ed]包含端點），給一個查詢陣列arr（要求出在arr[i]座標有多少個線段覆蓋

Concept:

算是經典的線段覆蓋，但是比賽的時候我有點忘記sweep line的作法ㄌ

但是反而想到Sort + Heap的方法：

Sort

先對線段flowers和查詢點people先排序

Heap

這邊的Heap是Min Heap，紀錄的是線段的結束座標

（因為會有開始座標很早且結束座標很晚的長線段，有可能會包含較晚開始且較早結束的短線段，如果指比對較早開始的線段的結束座標會有沒有pop到的情況，所以需要Heap來動態取出最早結束的線段座標，並檢查結束座標是否小於當前的查詢座標）

加入Min Heap的時機點：

當前線段的起始座標小於等於當前查詢座標並且結束時間點大於等於查詢座標（線段覆蓋住查詢點）

pop 時間點

當Heap的top的結束時間點比當前查詢座標還小：

代表整個線段已經在查詢座標之前了，這個線段不會覆蓋到查詢點

Solution:

實做的時候把people陣列當作回傳answer的陣列（因為已經把值複製到temp陣列了，不需要再用到people陣列，省一些空間）

#define F first
#define S second
typedef pair<int,int> pii;

class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {
        int n = flowers.size() , p_size= people.size();

        sort(range(flowers));
        vector<pii> temp(p_size);
        
        for(int i=0;i<p_size;i++){
            temp.push_back( {people[i] , i } );
        }
        sort(range(temp));

        int L_idx = 0;
        int Contain=0;

        priority_queue< int , vector<int> , greater<int> > pq;
        vector<int> ans;
        for(pii &P : temp){
            int posX = P.F;
            
            while( pq.size() && pq.top() < posX ){
                pq.pop();
                Contain--;
            }
            while( L_idx < n && flowers[L_idx][0]<=posX ){
                if( flowers[L_idx][1] < posX ){
                    L_idx++;
                    continue;
                }
                pq.push( flowers[L_idx][1] );
                L_idx++;
                Contain++;
            }

            people[ P.S ] = Contain;
        }

        return people;
    }
};

290th LeetCode Weekly Contest

Leetcode 290th 週賽

290th LeetCode Weekly Contest

Leetcode 290th 週賽

290th LeetCode Weekly Contest

Intersection of Multiple Arrays

Description:

Example:

Concept：

Solution：

Count Lattice Points Inside a Circle

Description:

Example:

Concept：

Solution：

Count Number of Rectangles Containing Each Point

Description :

Exmample:

Concept：

Solution:

Number of Flowers in Full Bloom

Description :

Example:

Concept:

Solution: